Weibull Distribution
Weibull Distribution describe by Advance Innovation Group, it will help you to have a primary knowledge about what is weibull Distribution.
Commonly used to model time-to-failure data. For example, a manufacturer is interested in calculating the probability that a part fails after one, two, or more years. It has wide application in engineering, medical research, finance, and climatology.
Weibull distribution is described by the shape, scale, and threshold parameters. The case when the threshold parameter is zero is called the 2-parameter Weibull distribution. It is defined only for non-negative variables.
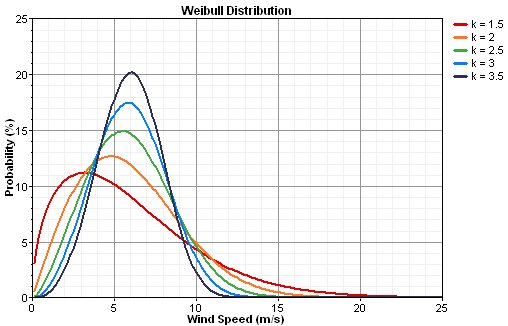
Depending on the values of the parameters, the Weibull Distribution can take various shapes.
One of the main advantages of this distribution is that it can take on the characteristics of other types of distribution making it extremely flexible in fitting different kinds of data. For example,
- The exponential distribution is a special case of Weibull distribution often used to study the scattering of radiation or wind speed.
- The Weibull distribution is an alternative to the normal distribution in the case of skewed data.
- If X follows a Weibull distribution, then Ln(X) follows an extreme value distribution. This distribution is used to describe extreme conditions, such as extreme wind-gust, extreme energy during earthquakes, or extreme stress.
When the shape parameter is 2, the Rayleigh distribution can be derived from the Weibull distribution.
The Weibull distribution is described by
Effect of the shape parameter
The shape parameter describes how your data are distributed. A shape of 3 approximates a normal curve. A low value for shape, say 1, gives a right-skewed curve. A high value for shape, say 10, gives a left-skewed curve.
Effect of the scale parameter
The scale, or characteristic life, is the 63.2 percentile of the data. The scale defines the position of the Weibull curve relative to the threshold, which is analogous to the way the mean defines the position of a normal curve. A scale of 20, for example, indicates that 63.2% of the equipment will fail in the first 20 hours after the threshold time.
Effect of the threshold parameter
The threshold parameter describes the shift of the distribution away from 0. A negative threshold shifts the distribution to the left, and a positive threshold shifts the distribution to the right. All data must be greater than the threshold. The 2-parameter Weibull distribution is the same as the 3-parameter Weibull with a threshold of 0. For example, the 3-parameter Weibull (3,100,50) has the same shape and spread as the 2-parameter Weibull (3,100), but is shifted 50 units to the right.
For more https://support.minitab.com/en-us/minitab/18/help-and-how-to

 Pranay Kumar
Pranay Kumar 





























Comments (0)
Facebook Comments