When shall we study Variance over Standard Deviation – or in first place Variance as we can arrive at Standard Deviation easily by taking the root of Variance ?

When shall we study Variance over Standard Deviation – or in first place Variance as we can arrive at Standard Deviation easily by taking the root of Variance ?

Shishu Pal Shishu Pal Apr 25, 2019 3182 0

When shall we study Variance over Standard Deviation – or in first place Variance as we can arrive at Standard Deviation easily by taking the root of Variance ?

When shall we study Variance over Standard Deviation – or in first place Variance as we can arrive at Standard Deviation easily by taking the root of Variance

The usage of Variance over Standard Deviation, why do we study Variance over Standard Deviation, when the Standard Deviation can be easily calculated by taking Square Root of the Variance, and is known to be the most robust method to calculate variation.

ONE THOUGHT ON “WHEN SHALL WE STUDY VARIANCE OVER STANDARD DEVIATION – OR IN FIRST PLACE VARIANCE AS WE CAN ARRIVE AT STANDARD DEVIATION EASILY BY TAKING THE ROOT OF VARIANCE ?”
Saif
JUNE 26, 2015 AT 10:59 AM
hi!!!!!!!
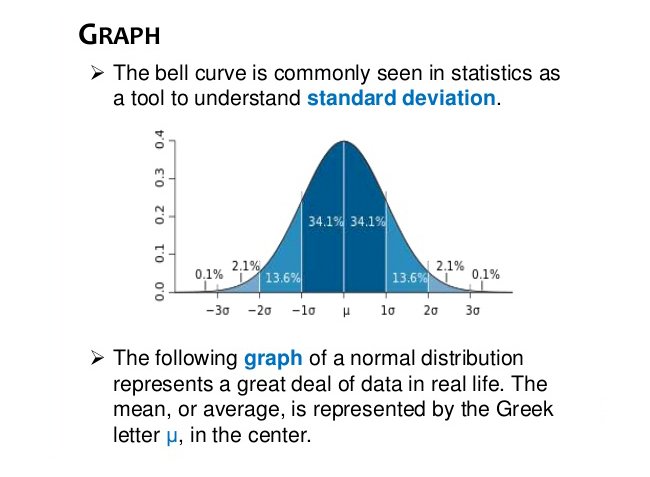
The standard deviation is the square root of the variance.
The standard deviation is expressed in the same units as the mean is, whereas the variance is expressed in squared units, but for looking at a distribution, you can use either just so long as you are clear about what you are using. For example, a Normal distribution with mean = 10 and sd = 3 is exactly the same thing as a Normal distribution with mean = 10 and variance = 9.
This is equivalent. Nonetheless, standard deviation is expressed in the same units as the variable whereas the units of the variance are those of the variable to the power two. This makes standard deviation easier to interpret.
thanks
Saif
LOG IN TO REPLY